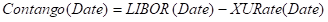Precious Metal Curve

From the Calypso Navigator, navigate to Market Data > Commodity Curves > Precious Metal Curve (menu action marketdata.CurveZeroPreciousMetalWindow).

 

Precious Metal Curves Quick Reference Configuration Requirements • Currency – The precious metal should be defined as a currency in the system. From the Calypso Navigator, navigate to Configuration > Definitions > Currency Definitions. • Currency Pair – Set up a currency pair for the precious metal and interest currency also in the Currency Definitions. • Reference Index – The precious metal requires a reference index. From the Calypso Navigator, navigate to Configuration > Interest Rates > Rate Index Definitions. Curve Underlying Instruments The curve requires Contango (FX Forward) and Swap underlying instruments. From the Calypso Navigator, navigate to Configuration > Market Data > Curve Underlyings, or in the curve application’s Underlyings panel, click New/Edit Underlying. Interest Rate Curve The precious metal curve requires an underlying interest rate curve. From the Calypso Navigator, navigate to Market Data > Interest Rate > Curves > Zero yield Curve. Curve Generation 1. Click New to start a new curve. 2. Select the quote instance to use in the curve generation (CLOSE, for example). 3. The Current checkbox is selected by default, meaning that when you save the curve, the system timestamps the curve with the current date and time. Clear the Current checkbox to enter a back-dated curve. You can modify the date and time fields. 4. Definition Panel — select the following to define the curve: currency, reference index, tenor, “Generate from instruments” should be checked, holiday calendar, interpolator, “PreciousMetal” generation algorithm, “CurveZeroPreciousMetal” curve type, Pricing Env, underlying interest curve. 5. Underlyings Panel — select the underlying instruments. 6. Quotes Panel — enter quotes manually, use quotes from the quote set, or use real-time quotes. 7. Points Panel — click Generate to generate the points. 8. Click Save, enter a name for the curve, and click OK. Pricer Configuration Assign a precious metal curve to a pricing environment in the Discount Curves or Forecast Curves panel in the pricer configuration. From the Calypso Navigator, navigate to Market Data > Pricing Environment > Pricer Configuration.

 

1. Creating Curve Underlyings

You can set up underlying instruments before creating the curve, or while you are creating the curve. From the Calypso Navigator, navigate to Configuration > Market Data > Curve Underlyings, or in the curve application’s Underlying panel, click New/Edit Underlying.

In the Curve Underlying Window, create a list of Contango instruments (tenors from TN, 1W, 1M, to 1Y).

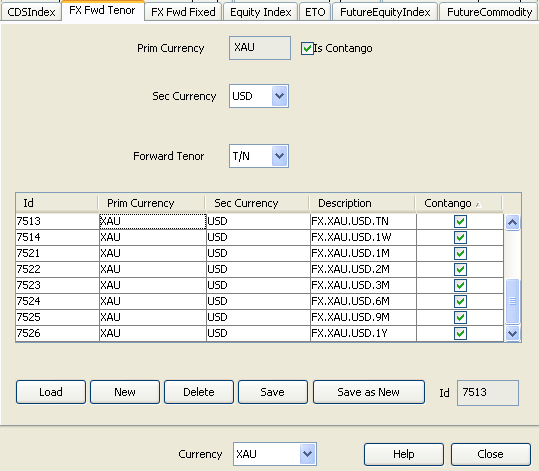
In the Curve Underlying Window, create a list of swaps (tenors from 2Y, 3Y, to 15Y) to model Lease Rate Swap. 

 

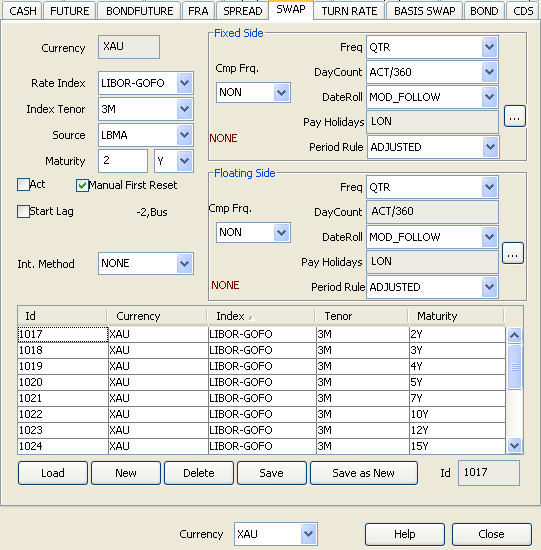
2. Creating a Curve

Click New to start a new curve.

Select the following to define the curve: currency, reference index, tenor, “Generate from instruments” should be checked, holiday calendar, interpolator, “PreciousMetal” generation algorithm, “CurveZeroPreciousMetal” curve type, Pricing Env, underlying interest curve.

»

Click ... to add the “PreciousMetal” generator:

»

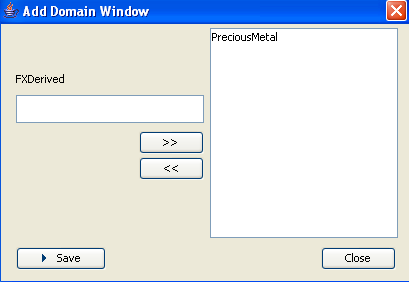
Enter the generator name in the text field.

»

Click >> to add the generator name to the panel on the right.

»

Click Save to add it to the generation algorithm list.

 

2.1 Underlying Panel

Click the Underlying tab. Select the underlying instruments to use in the curve.

»

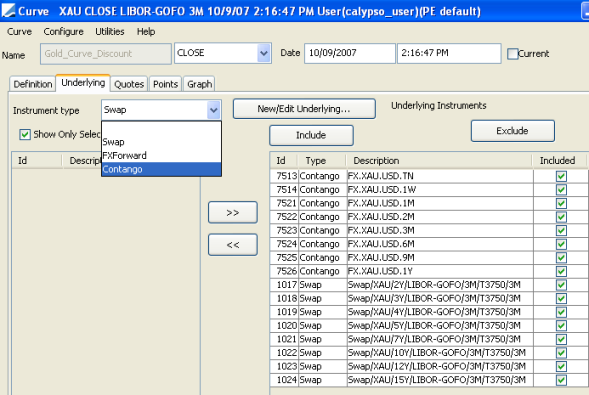
Select the instrument type, and the panel below displays the list of available instruments. The panel is blank if you have not set up any instruments. Click New/Edit Underlying to create new instruments.

»

Select instruments and click >> to add them to the instrument list in the right panel.

 

2.2 Quotes Panel

Click the Quotes tab.

You can enter quotes and Save Quotes to the quote set associated with the selected pricing environment.

The quotes may be automatically populated if you are running a real-time feed, or they may be populated from the quote set associated with the selected pricing environment.

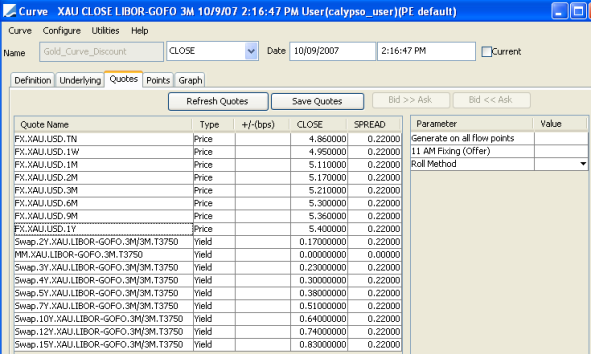
You can create one of the following types of curves:

»

Discount Curve — this curve is created by default.

In computation, Contangos use Close while Swaps use (Close - 0.5*Spread)

»

Forecast Curve — set the parameter “11 AM Fixing (Offer)” to “true” to create the forecast curve.

In computation, Contangos use (Close + 0.5*Spread) while Swaps use Close.

You can set the following parameters in the Quotes panel when you use the PreciousMetal generator.

Parameter	Description	Default Value
Generate on all flow points	Set to “‘true” to generate curve points at each flow date of multi-period instruments, such as swaps.	false
11 AM Fixing (Offer)	By default, the precious metal generator creates a discount curve. Set this parameter to “true” to create a forecast curve.	false
Roll Method	You can select the roll method. For example, you create a curve instance on T0. On T1 you price a trade. • Roll Points — Curve points are rolled forward when pricing. The points are the same on T1 as on T0. • Regenerate — Curve points are regenerated when rolled. The points are regenerated on T1 using quotes from T0.	Roll Points

 

2.3 Points Panel

Click the Points tab. Click Generate to generate the points.

 

2.4 Save Curve

Click Save in the bottom of the curve window. Enter a name for the curve, and click OK.

 

3. Pricer Configuration

 Ⓘ   [NOTE: you must have CurveZeroPreciousMetal defined in the curveZeroType domain in order to assign the curves in the pricer configuration. From the Calypso Navigator, navigate to Configuration > System > Domain Values]

 

From the Calypso Navigator, navigate to Market Data > Pricing Environment > Pricer Configuration.

Click Load, select the pricer configuration name, and click OK.

 

3.1 Discount Curve

»

Add the Precious Metal discount curve in the Discount Curves panel.

»

Click the Discount Curves tab to bring it to the front.

»

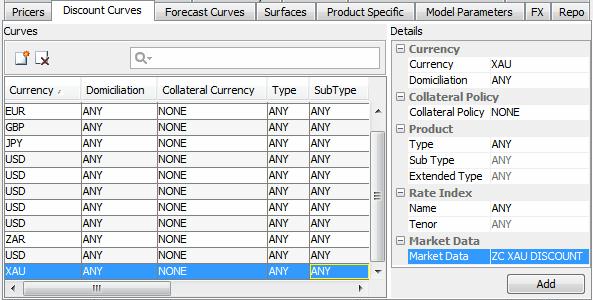
Select the currency, and set the index to ANY.

»

Click ... to select the curve.

»

Click Add to add the curve to the list.

»

Click Save to save the pricer configuration.

 

3.2 Forecast Curve

Add the Precious Metal forecast curve in the Forecast Curves panel.

 Ⓘ   [NOTE: It is assumed that a USD discount curve is already set up and added to the pricing environment]

»

Click the Forecast Curves tab to bring it to the front.

»

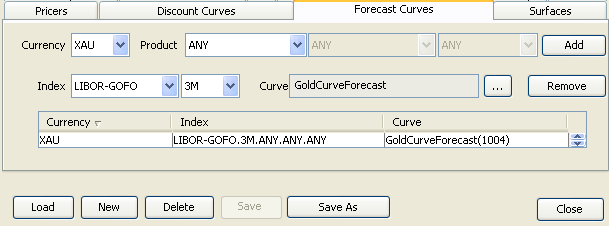
Select the currency, product type or ANY, index, tenor.

»

Click ... to select the curve.

»

Click Add to add the curve to the list.

»

Click Save to save the pricer configuration.

 

4. Analytics

This section details the construction methodology for the Gold Interest Rate curve based on the instruments TNContango, Contangos and LeaseRateSwaps.

 

Sample Inputs

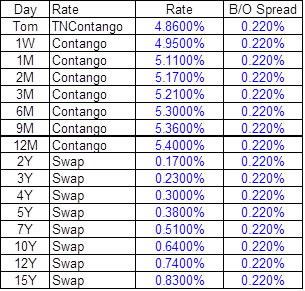
All pillar points are out of Spot (except for Tom, which is 1 business day after today)

Resultant Discount Function

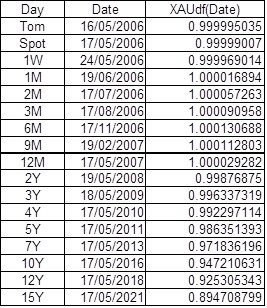
Note the possibility of having negative interest rates.

 

Notations

Today: Today

Tom: The next Business Day after Today

Spot: Two Business Days after Today

Date: Some Date

USDdf(Date): The zero coupon USD discount function from Today to Date

XAUdf(Date): The zero coupon XAU discount function from Today to Date

The object is to show how to construct XAUdf(Date) for a set of Pillar Dates.

Days(Date1,Date2): Number of Calendar Days from Date1 to Date2

Gold(Date):The Forward Price of Gold at Date.

For instance Gold(Spot) is just the Spot price of Gold.

We have the following relationship between Gold(Date), XAUdf(Date) and USDdf(Date):

 

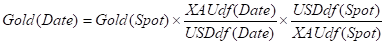
4.1 Discount Curve out to Spot based on TNContango

The Discount Curve for Tom and Spot is based on the one input TNContango.

TNContango: The contango from Tom to Spot.

This defines the relationship between the Tom price of Gold and the Spot price of Gold:

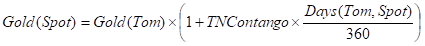
This relationship is used to back-out a Rate called the TNRate, which is then used as the fixed Gold Rate from both Today to Tom, and from Tom to Spot.

 

TNRate: XAU in XAU Rate from Tom to Spot

So TNRate is defined from the XAUdf() as:

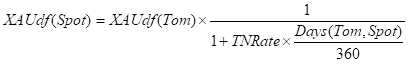
So solving for TNRate using the TNContango definition and the relationship between Gold(Tom) and Gold(Spot) we have:

 

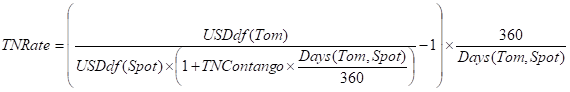
The TNRate is now used to calculate both discount factors for Tom and Spot.

 

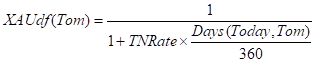
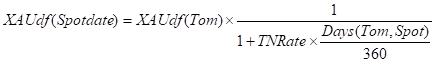
4.2 Discount Curve based on Contangos

Gold Contangos are rates used by the Market to define the Gold Forward Curve.

Contango(Date): The XAU Contango from Spot to Date

This defines the relationship between the Spot price of Gold and any Forward Price as:

Using the general relationship between Gold(Spot) and Gold(Date) above we have immediately:

 

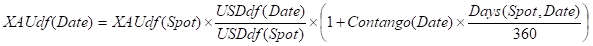
4.3 Discount Curve based on Lease Rate Swaps

The gold swap is a market instrument for trading gold interest rate exposure. The standard Gold Lease Rate Swap is Quarterly – Quarterly, with quarterly coupons paid in gold on an Actual 360 day basis

Swap(i): The quoted (Offer) fixed rate for a swap with maturity i Quarters

BidOffer(i): The Bid/Offer on the traded i Quarters Swap

Date(i): the date of the ith Quarter swap date, Date(0)=Spot

days(i)=Date(i)-Date(i-1)

XAUdf(i)=XAUdf(Date(i))

(e.g. Swap(12) refers to the 3 year swap rate, XAUdf(12) is the 3 year Discount Factor)

 

Assume we have the XAU discount curve built out to n Quarters based on some other XAU Rates inputs (i.e. Gold Contangos). So for the nth Quarter from the definition of Swaps we have:

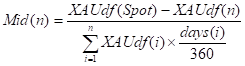
We also have a Mid(i) for each quoted Lease Rate Swap, as

Mid(i)=Swap(i) – BidOffer(i)/2

For all remaining Quarters we interpolate the Mid(i), so if Mid(m) and Mid(n) are known, and m<i<n, then we linearly interpolate on the quarters like:

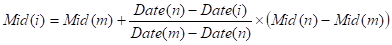
So we can assume we have a Mid(i) for each quarter. Then given that we now have a strip of Mid(i), i=1,2,…, the XAU discount curve is backed out iteratively so that

 

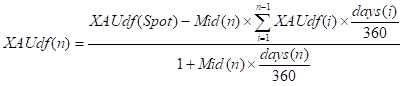
4.4 Appendices

 

Appendix A - XAU in XAU Definition

The XAU in XAU is a ACT/360 Simple Rate. Let

XXRate(Date) : the XAU in XAU ACT/360 Rate from Spot to Date

Then it follows that given XAUdf(Spot) we can construct the XAUdf(Date) as:

 

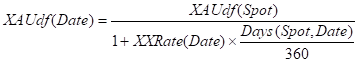
Appendix B - XAU in USD Definition

It is sometimes simpler when depositing Gold to earn an interest payment payable in USD (rather than say XAU). The interest payment is referenced off the current Spot Price of Gold.

XURate(Date): The XAU in USD Rate from Spot to Date

For instance, if the deposit is 1oz of Gold, to be redeemed at Date, then the USD Interest payable at Date would be:

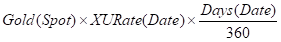
That is, XURate(Date) represents the simple ACT/360 interest payable in USD on 1oz of Gold where the USD Notional is Gold(Spot) Dollars. From arbitrage considerations, it must be equivalent to receive either a XAU in USD interest payment or XAU in XAU Interest payment, hence we have the following equivalence

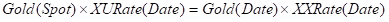
That is, a XAU in USD payment must be the same as a XAU in XAU payment converted to USD at the forward Date.

To construct the XAUdf(Date) from the XURate(Date) we can either solve the above equation, or more simply note that 1oz received at Spot, must be equivalent to the present value of 1oz received at Date plus the present value of XAU in USD interest paid on that 1oz. That is:

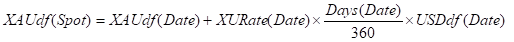
So it follows that given we have XAUdf(Spot) then we can construct XAUdf(Date) for any given XURate(Date) as:

 

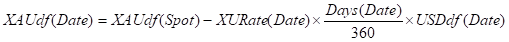
Appendix C - XAU in USD and Contango Relationship

We have the following equivalence. We can either invest 1oz of Gold to some Date and receive XAU in USD Interest, and then convert the 1oz at that Date to USD, or convert our 1oz at Spot and earn Libor out to Date. Let

LIBOR(Date): The ACT/360 Simple USD Rate from Spotdate to Date

Then the above equivalence is

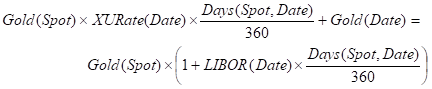
Rewriting Gold(Date) in terms of Contango(Date) and dividing by Gold(Spot) gives the relationship: