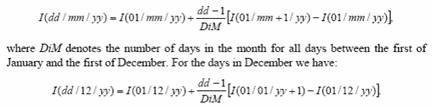Capturing Inflation Swap Trades
Inflation swaps are based on inflation indices. Inflation is defined as the percentage increase or decrease in some index of prices.
|
Inflation Swaps Quick Reference
|
1. Defining Inflation Rate Indices
From the Calypso Navigator, choose Configuration > Interest Rates > Rate Index Definitions.
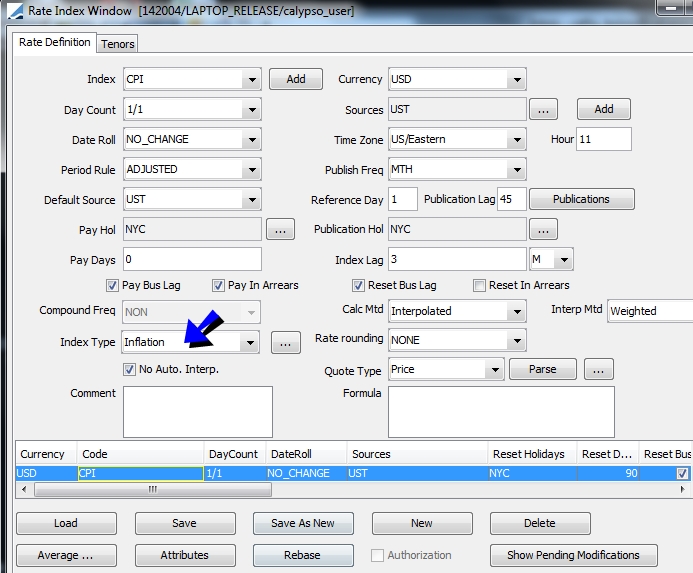
The Rate Definition panel is selected by default.
| » | Select the rate index from the Index field, and enter its details. Select Inflation from the Index Type field. Fields specific to inflation indices are described below. |
You can click Add to add it, if it does not exist.
| » | Click Attributes and set the following attributes. You can click ... to add an attribute if it does not exist. |
Note that the attributes and their values are case sensitive.
IndexCalculator = InflationIndexKerkhof
Use Inflation Ref Date = True (Only if the index is defined as Index Level but uses a forecast curve whose points are reference (settle) dates instead of inflation dates (actual dates on which inflation is set))
| » | Click Save to save your changes. |
| » | Then select the Tenors panel to define tenors for the rate index, and click Save to save your changes. |
For zero coupon swaps, you can set the tenor to “0D”.
For year on year swaps, the tenor is used to select reference dates for the resets. For example, if the tenor is “1Y”, and the rate index setting in advance, the first reset is taken from 1 year before plus lag: Index Start Date = Index End Date – Tenor – Index Lag.
| » | You can click Rebase to rebase the index level as needed. |
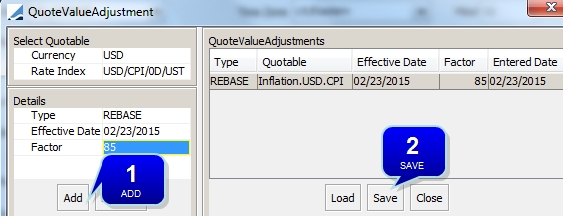
Step 1 - Enter an effective date and a rebase factor in percentage.
Step 2 - Click Save.
Fields Details
|
Rate Index |
Attributes |
||||||
|
Index Type |
Select Inflation. |
||||||
|
Calc Mtd |
Select the calculation method:
|
||||||
|
Interp Mtd |
Only appears for the Interpolated calculation method. The only option is "Weighted" - Index levels are interpolated using the following formula: For example, to calculate an interpolated May 12th CPI index level, which has a 3 month lag:
|
||||||
|
No Automatic Interpolation |
This checkbox is not related to the interpolation method of Inflation rates. When checked, there is no automatic interpolation applied to stub periods, otherwise stub periods are automatically interpolated. |
||||||
|
Publish Freq |
Select the frequency at which the rate is published. For Inflation indices, select a publication frequency, enter a reference day and a publication lag.
The reference day is the day of the month when the inflation is effective, and the publication lag is the time lag between the effective date of an inflation level and its actual publication. You can click Publications and generate the dates to make any modification if needed. Otherwise the reference day and publication lag are used to determine the publication dates.
Ⓘ [NOTE: The system does not support end-of-month reference days 29, 30, and 31. This restriction also pertains to the Publications Dates window described above when modifying the Reference Date fields.] |
||||||
|
Index Lag |
Enter the index lag, usually 3M. |
2. Defining Market Data
Inflation curves are defined from the Calypso Navigator using Market Data > Interest Rate Curves > Inflation Curve. You can create a derived inflation curve from underlying instruments with various methods for applying seasonal adjustments – The seasonal adjustments can be retrieved from a seasonality curve.
Sample Inflation Curve
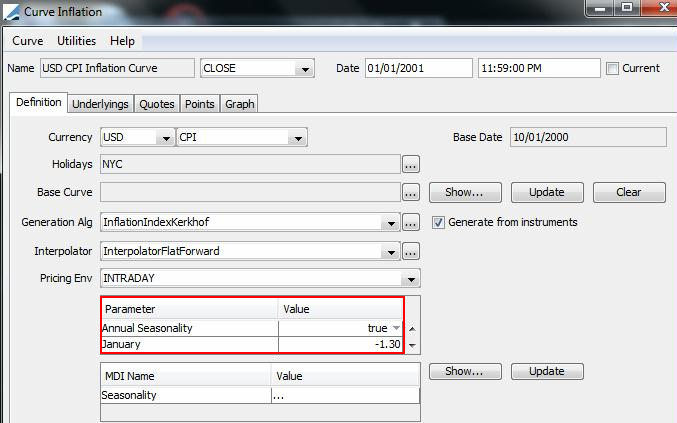
| » | Choose Help > Inflation Curve Help for complete details. |
3. Capturing Zero Coupon Swap Trades
In a zero coupon swap, the parties exchange one cashflow—at maturity. A simple example is a swap with a fixed rate leg and an inflation-indexed leg. The fixed leg payer pays notional plus a coupon of the compounded value of the fixed rate. The inflation-indexed leg payer pays notional plus a coupon reflecting the percentage change in the inflation rate.
Choose Trade > Interest Rates > Swap to open the Swap worksheet, from the Calypso Navigator or from the Trade Blotter.
Sample zero coupon swap trade.
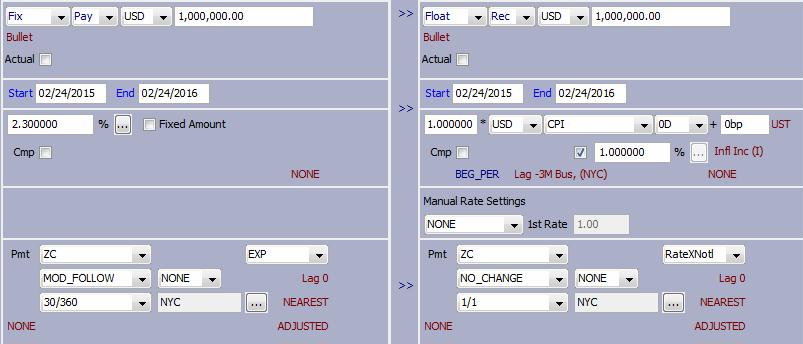
| » | On the fixed side, set the payment schedule to ZC. If the fixed rate is to be compounded annually, select EXP or ACC from the adjacent field. |
Interest = Notional * ((1 + Rate)^t[n] - 1).
| – | For EXP: t[n] = Current Coupon Period n |
| – | For ACC: t[n] = Total Period from Coupon 1 through n. |
| » | On the floating side, select the inflation index with “0D” tenor. The default lag is retrieved from the rate index. If the inflation lag payment formula does not use a period, select RateXNotl. |
You can set a fixed rate in the "%" field to reflect the change in inflation level.
| » | In the Manual Rate Settings, you can select “Init Level” or "Init Level Date". |
| – | Init Level |
Enter the base index level and initial level date (reference date).

The level date is in the form “MM/DD/yyyy”, where DD is the Reference Day specified in the Rate Index Definition.
| – | Init Level Date |
Enter the level date - It is the publication date corresponding to the first reset (first reset date + publication lag). The system will retrieve the corresponding index level from the quotes if available, or will compute it from the inflation curve.

Index and Resets Override
If you double-click any red label, you can overwrite the index defaults in the Index and Resets panel.
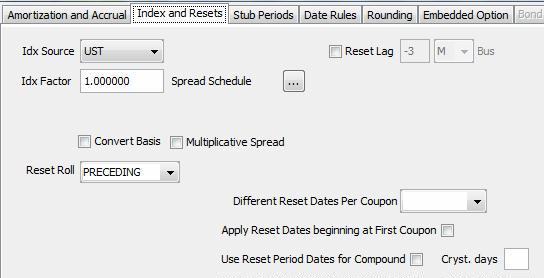
| » | You can check "Multiplicative Spread" to have a multiplicative spread rather than an additive spread. |
Additional Inflation Parameters
If you double-click any red label, you can set additional parameters in the Inflation panel.
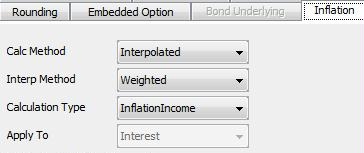
| » | Select the calculation method: |
| – | Interpolated - Daily index levels are interpolated between reference dates. |
| – | IndexLevel - Index levels are not interpolated between reference dates. |
| » | The only "Interp Method" option is "Weighted", which is only available for the Interpolated calculation method. |
| » | Select the calculation type to apply inflation level changes to cashflows: |
| – | InflationIncome - [(Final Level / Initial Level) - 1] |
| – | InflationIndexation - [Final Level / Initial Level] |
| » | Select whether to apply the InflationIndexation calculation type to just Interest, or both Interest and Principal. |
Cashflows
In the cashflows panel, you can view the projected index levels.
![]()
Right-click a cashflow and select Sample Dts to view the index levels used to compute the projected rate.
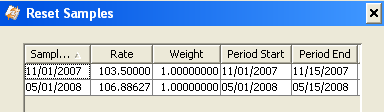
You can also customize "Final Infl Reset Date” and “Init Infl Reset Date” as needed.
Since the index calculator InflationIndexKerkhof requires a specific reference date to pick up the projected inflation level from the curve, the following columns are also available:
| • | Initial Reference Number Projection Date |
| • | Final Reference Number Projection Date |
| • | Projected Initial Reference Number |
| • | Projected Final Reference Number |
4. Capturing Year-on-Year Swap Trades
In a year-on-year inflation swap, payments are made annually. In a simple example, with a fixed rate leg and an inflation-linked leg, the fixed side pays an annual coupon reflecting the fixed rate. The inflation-linked leg pays the change in the inflation rate.
Choose Trade > Interest Rates > Swap to open the Swap worksheet, from the Calypso Navigator or from the Trade Blotter.
Sample year-on-year swap trade.
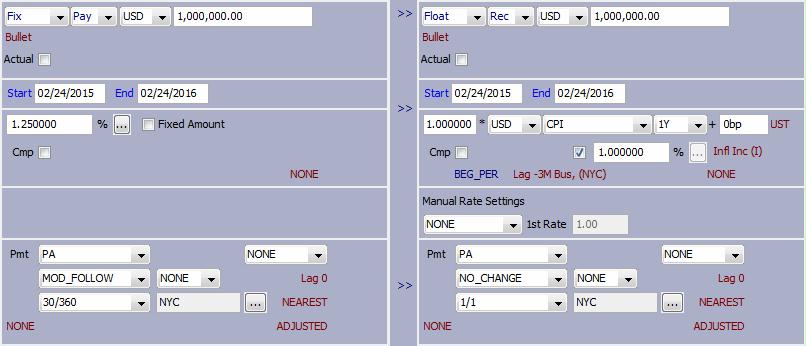
| » | The tenor is used in selecting the reference dates for the resets. For example, if the tenor is 1 Year with setting in advance, the first reset is taken from 1 year prior plus the index lag. The general formula is Index Start Date = Index End - Tenor - Index Lag. |
You can specify the same fields as for Zero Coupon Swap Trades.
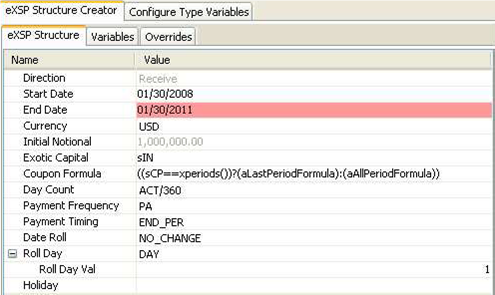
5. Capturing OATi-like Swap Trades
These types of swaps are captured using exotic structures.
Choose Trade > Interest Rates > Swap to open the Swap worksheet, from the Calypso Navigator or from the Trade Blotter.
5.1 OATi-like Swap Type Setup for a Given Index where Index Initial is a Parameter
Defining the same structure for different indices (in this example using REUTERS screen name) may be the most convenient setup. In this example the user can enter a constant number for the index initial.
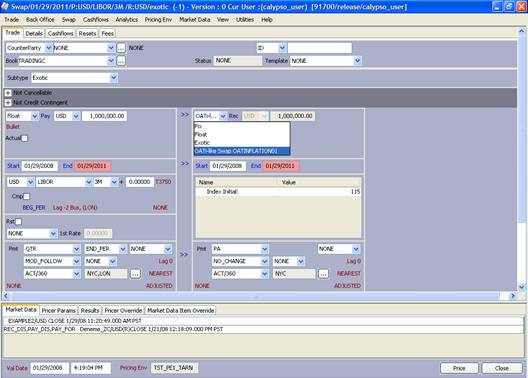
Below please find the details how to capture an exotic Type for OATi-like Swaps. In the structure there are two different formulas. The first formula is applicable to all the periods except the last one and the second formula is applicable to the last period only.
So the coupon formula checks if it is the last period and changes the applicable formula accordingly.
Coupon Formula: ((sCP==xperiods())?(aLastPeriodFormula):(aAllPeriodFormula))
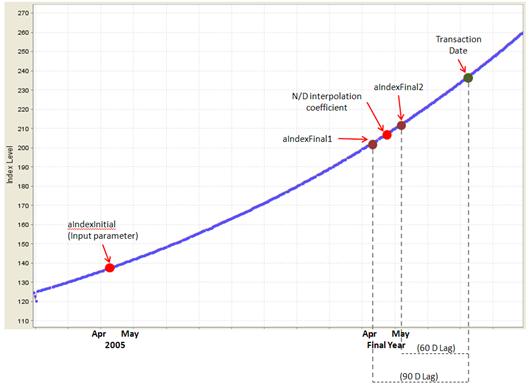
Below graph shows some of the terminology used in variables.
|
Variable Definition |
Formula |
|
aLastPeriodFormula |
(((1.00/100.00)*((aIndexFinal1+(aInterpolationCoef*(aIndexFinal2- aIndexFinal1)))/aIndexInitial))+((aIndexFinal1+(aInterpolationCoef*(aIndexFinal2- aIndexFinal1)))/aIndexInitial))-1.00 |
|
aAllPeriodFormula |
(1.00/100.00)*((aIndexFinal1+(aInterpolationCoef*(aIndexFinal2- aIndexFinal1)))/aIndexInitial) |
|
aIndexFinal2 |
Use an exotic variable: Second Point (60D Lag) of interpolation for the Index Final |
|
aIndexFinal1 |
Use an exotic variable: First Point (90D Lag) of interpolation for the Index Final |
|
aIndexInitial |
Manual input for the Index Initial: This is shown in Type as a parameter |
|
aInterpolationCoef |
N/D interpolation coefficient: (xMonthDay(0.00,0.00)-1.00)/xMonthDays() |
5.2 OATi-like Swap Type Setup for a Given Index with Constant Lag of Initial Index
This type definition assumes a constant lag between the “index initial” date and the first “index final” date. For example if the final index will be calculated using the index of MONTH and MONTH+1 of YEAR and index initial will be calculated using the index of MONTH and MONTH+1of YEAR-2 than this structure type does not require the user to put the initial level but pulls it directly from the appropriate quote.
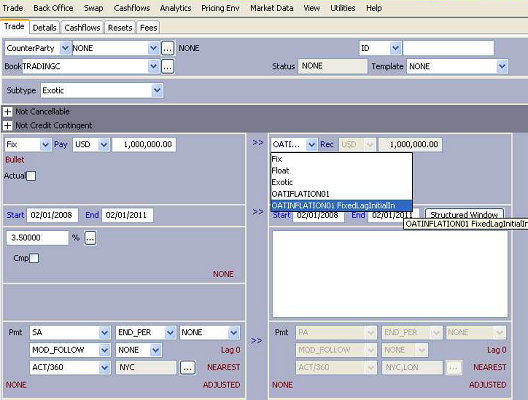
Below please find the details how to capture a Type for OATi-like Swaps with a constant lag of index initial. In the structure there are two different formulas. The first formula is applicable to all the periods except the last one and the second formula is applicable to the last period only. In this type please note that the index initial is interpolated and fixed using a pair of time series variables and xwavg(TSeries,1,1) functions, so that index initial remains same during the cash flows.
The coupon formula again checks if it is the last period and changes the applicable formula accordingly.
Coupon Formula: ((sCP==xperiods())?(aLastPeriodFormula):(aAllPeriodFormula))
|
Variable |
Definition |
|
aLastPeriodFormula |
(((1.00/100.00)*((aIndexFinal1+(aInterpolationCoef*(aIndexFinal2 – aIndexFinal1)))/aIndexInitial))+((aIndexFinal1+(aInterpolationCoef*(aIndexFinal2-aIndexFinal1)))/aIndexInitial))-1.00 |
|
aAllPeriodFormula |
(1.00/100.00)*((aIndexFinal1+(aInterpolationCoef*(aIndexFinal2- aIndexFinal1)))/aIndexInitial) |
|
aIndexFinal2 |
Use an exotic variable: Second Point (60D Lag) of interpolation for the Index Final |
|
aIndexFinal1 |
Use an exotic variable: First Point (90D Lag) of interpolation for the Index Final |
|
aIndexInitial |
Manual input for the Index Initial: This is shown in Type as a parameter |
|
aInterpolationCoef |
N/D interpolation coefficient: (xMonthDay(0.00,0.00)-1.00)/xMonthDays() |
|
aIndexInitial |
aIndexInitial1+aInterpolationCoef*(aIndexInitial2-aIndexInitial1) |
|
aIndexInitial1 |
xwavg(tIndexInitialCONS1,1,1) : Fixing |
|
aIndexInitial2 |
xwavg(tIndexInitialCONS2,1,1) : Fixing |
|
tIndexInitialCONS1 |
Use an exotic variable: First Point (450D Lag) of interpolation for the Index Initial |
|
tIndexInitialCONS2 |
Use an exotic variable: Second Point (420D Lag) of interpolation for the Index |
6. Capturing UK RPI Swap Calypso Setup
UK RPI Swap is another inflation based trade that can be captured using the eXSP window.
Choose Trade > Interest Rates > Swap to open the Swap worksheet, from the Calypso Navigator or from the Trade Blotter.
6.1 UK RPI Swap with Inflation Based Compounding
Both legs of the swap are actually zero coupons. However one of the legs should be defined as a recursively growing rate at each period. Therefore this leg will be declared as a periodic coupon pay such as PA. The goal is to create the periodic product of all the rates and return the product as a single rate for the final period. The calculated inflation based rates will be multiplied with a vector where the last entry is 1 and the rest of the entries are 0. (i.e. [0,0,0,…,1]).
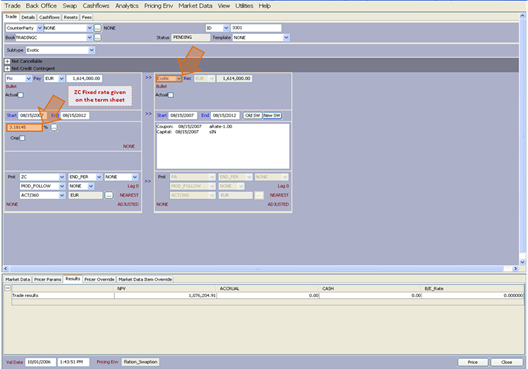
In the snapshot below please note the final rates after the multiplication with the [0,0,0,0,1] vector.
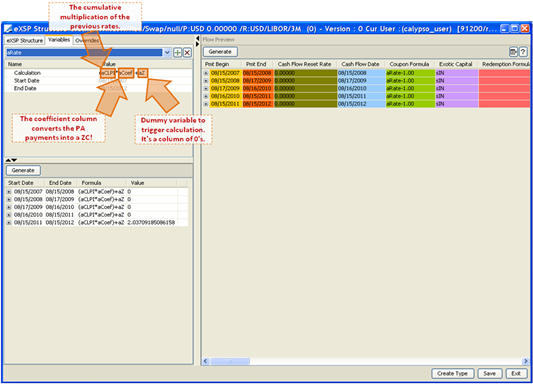
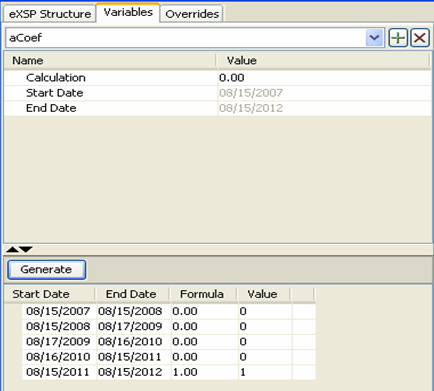
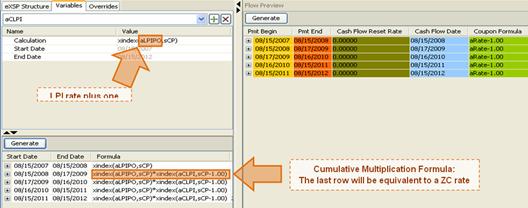
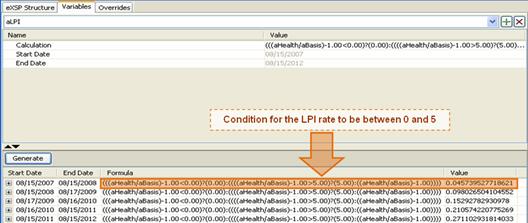
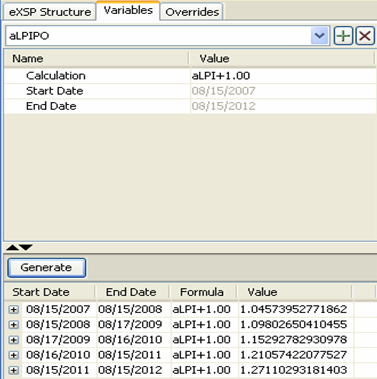
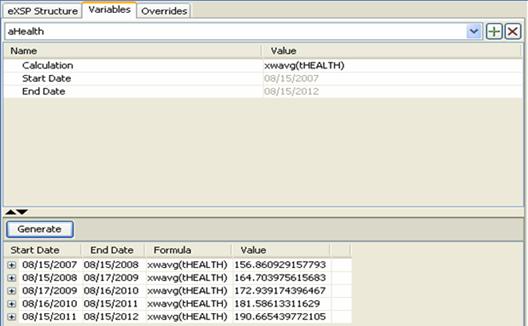

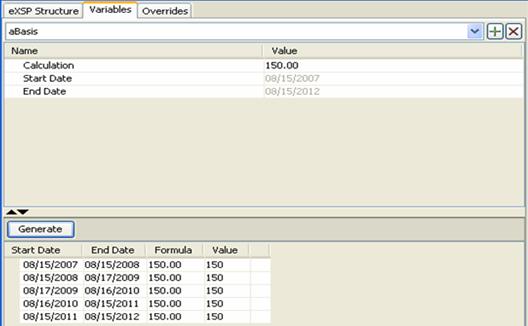
Below table summarizes the rest of the variables used in the structure.
| Variable | Formula |
|---|---|
|
aHealth |
xwavg(tHEALTH) |
|
tHEALTH |
qHEALTH: Exotic Quotable Variable that refers to the related inflation index – Note: You must replace qHEALTH with xinfl(qHEALTH) in all formulas. |
|
aBasis |
150 (a preferred constant Index Level for the initial level) |